MATEMATICAS: TEMA:Operaciones con monomios y polinomios

OPERACIONES CON MONOMIOS Y POLINOMIOS

Monomio: Un monomio es una expresión algebraica que consta de un solo termino
Ej: 3a

Polinomio: es una expresión algebraica  que tiene mas de un termino
Un binomio es un polinomio que tiene dos términos.
Un trinomio es un polinomio con 3 términos
Binomio: a+b
Trinomio: a+b+c

Monomio esta formado por números y letras separadas por signos de multiplicación o división. En álgebra no es necesario colocar el signo por, Ejemplo: 2abc/3

El grado absoluto de un polinomio es el grado de su termino de mayor grado
Ejemplo: x^4-5x^3+x^2-3x  el primer termino es de cuarto grado, el grado absoluto del polinomio es el cuarto

Términos semejantes: dos o mas términos son semejantes cuando tienen la misma parte literal osea las mismas letras y  igual exponentes, Ejemplo: 3a+2a=5a

Ejercicios:

1.  x+2x
2. -9m-7m
3. 1/3 xy+1/6xy
4. 7a-9b+6a-4b
5. -81x+19y-30z+6y+80x+x-25y

Respuestas: 1. 3x, 2. -16m, 3. 1/2xy, 4. 13a-13b, 5. -30z

SUMA: Se colocan los polinomios unos debajo de otros, se deben  ordenar con relación a una letra.

Ejercicios: 

1. -11m, 8m

2. 7a-4b+5c; -7a+4b-6c

3. 2a+3b; 6b-4c;-a+8c

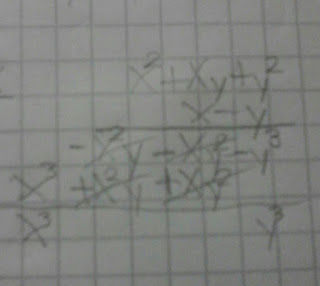
4. X^3+xy^2+y^3; -5x^2y+x^3-y^3; 2x^3-4xy^2-5y^3

Respuestas:

1. -3m
2.-c
3.a+9b+4c
4. (ver imagen 1)

RESTA: Se ubican los polinomios lo mismo uno debajo del otro Y se procede a restar hay que ubicar un polinomio debajo del otro  teniendo en cuenta el exponente y literal.

Ejercicios:

1. x^2+y^2-3xy resta -y^2+3x^2-4xy
2. x^3-x^2+6 resta 5x^2-4x+6

Respuestas:

1. -2x^2  +2y^2 +xy
2. x^3 -6x^2  -4x

MULTIPLICACIÓN:  En la multiplicación el orden de los factores no altera el resultado
los factores de un producto pueden agruparse de cualquier modo
Al multiplicar "signos iguales dan + y signos diferentes dan -
Para multiplicar potencias  de la misma base se suman los exponentes. Ejemplo:  2a^2x3a^3= 6a^5

Ejercicios:

1. 2x^2 por -3x    
2. -5x^3y por xy^2
3.  3x^3-x^2 por -2x

Respuestas:

1. -6x^3
2. -5x^4y^3
3. -6x^4+2x^3

DIVISIÓN: Es una operación que tiene como objetivo, dado el producto de dos factores (dividendo) y uno de los factores  (divisor) hallar otro factor (cociente).

Ley de los signos: signos iguales dan + y signos diferentes -

Ley de los exponentes: Para dividir potencias de la  misma base se deja la misma base y se le pone dr exponente la diferencia entre el exponente del dividendo y el exponente del divisor
Ejemplo: a^5/a^3=a^5-3=a^2

Ejercicios:
1. a^m+3 entre a^m+2

Respuesta:
1. a

Todo numero elevado a la 1 da el mismo a^1=a

División de polinomios por monomios: se divide cada uno de los términos del polinomio por el monomio separando los cocientes parciales con sus propios signos.

Ejercicios:

1.a^2-ab entre a
2. 3x^2y^3-5a^2x^4 entre -3x^2

Respuestas:

1. a-b
2. -y^3+5/3 a^2x^2


Realizado por: Frank Cañas